Big O Notation and an example at Amazon scale

In computer science, big-o-notation describes how the runtime of an algorithm scales as it’s input size gets bigger. This matters a lot, specially when you’re dealing with the scale of a company like Amazon.

What is Big O Notation

big-o-notation is a tool used in fields like mathematics and computer science to describe how a function scales according to it’s input. In software development, it is normally used to describe how the runtime of an algorithm will scale as it’s input size grows. Take the following function for example:

def printNumber(n: int):
    print(f"The number you entered is ${n}")

This function takes a number n as it’s input and prints it to the screen. This algorithm runs in constant time, because while n grows in value approaching infinity, the runtime of this algorithm will stay the same, because it always makes the same amount of work. We can say this algorithm has a Time complexity of $O(1)$.

Now let’s consider the following algorithm:

def printNumbers(n: int):
    for i in range(n):
        print(i)

This algorithm runs in linear time, because it’s runtime increases linearly as n grows up to infinity. To put it simply, if it takes 1 ms to run this function when $n=1$, it will take roughly 1000 ms to run when $n = 1000$. We can say this algorithm has a time complexity of $O(n)$.

If we plot both a linear function $f(x)$ and a constant function $g(x)$, there will always be a value $x$ from where $f(x) > g(x)$.

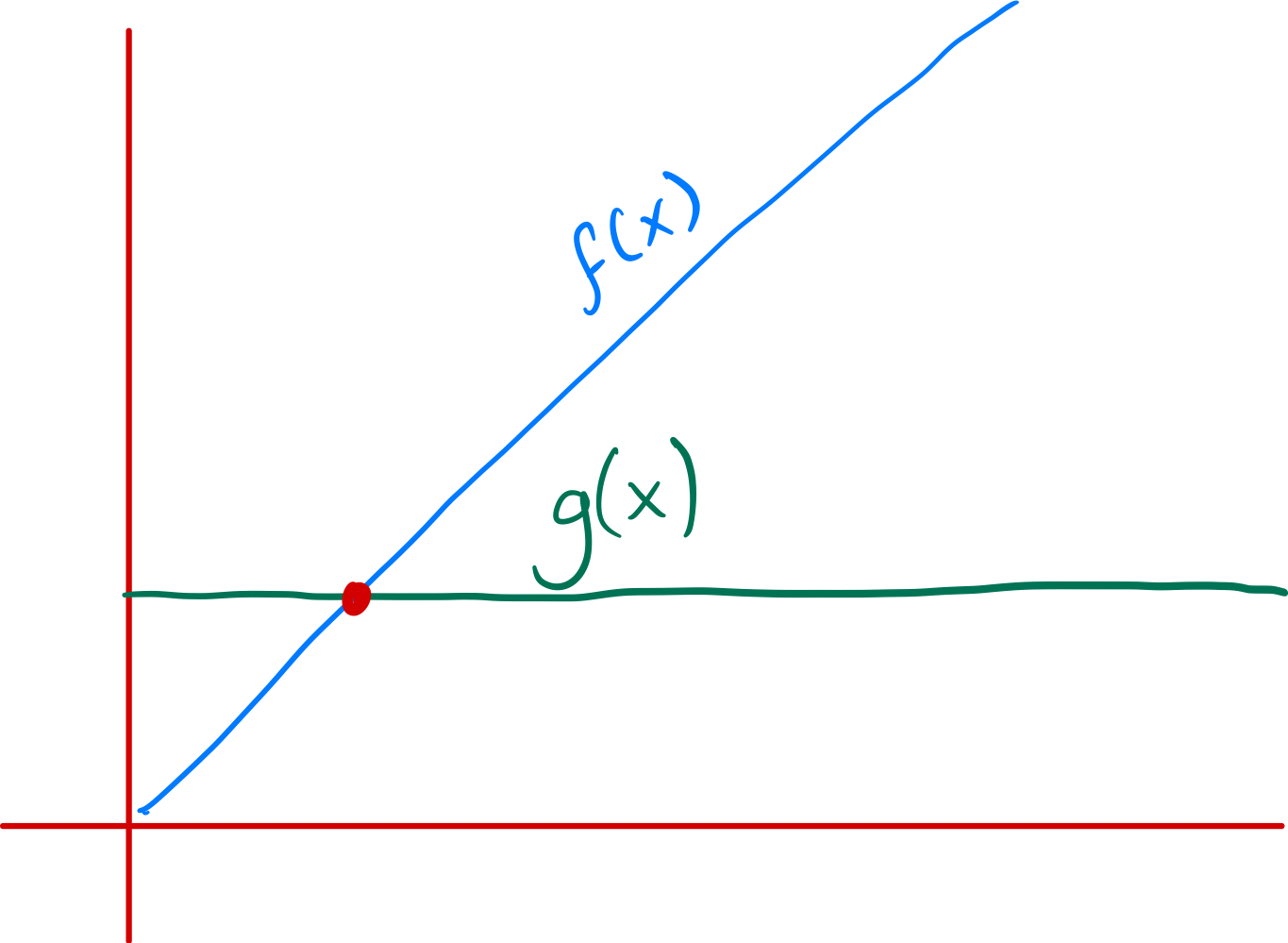
As you can see, no matter how separate the initial points of the functions are, eventually the value of $g(x)$, the constant function, will be lower than the value of $f(x)$, the linear function. Remember this functions are representing an algorithms runtime, so lower is better.

What does Amazon have to do with this?

Amazon is a Cloud Company first, with AWS accounting for most of it’s revenue. They sometimes need to transfer huge amounts of data from a customer to it’s servers, a process which you can imagine takes $O(n)$ time. The more data there is, the more time it will take for it to be sent to Amazon’s data-centers. When you’re working with Petabyte|petabytes and petabytes of data, $O(n)$ may still be too slow.

Amazon found a way around this problem, a way to transfer data at $O(1)$ time! How did they do this? What was the clever algorithm they discovered to transfer data in constant time? The answer may be a little bit surprising: trucks.

AWS Snowball

Yes, you read right, trucks. Amazon sends a truck and physically loads the customer’s data all at once. It takes the drives from the customer to it’s data-centers with a service they call AWS Snowball, and it takes (roughly) the same amount of time regardless of how much data you move, aka $O(1)$.

I found this very clever and funny, moving the drives physically would have to be faster at some point, and Amazon has clearly found themeselves past the point in the previous graph, where physically moving the drives is now faster than transfering the data through the internet.

Disclaimer

This isn’t really $O(1)$, since you still have to move data from one drive to another even if they are right next to each other physically, but this is practically a lot faster than sending the data over the internet, and while technically still $O(n)$, it is still a big improvement for higher values of $n$.